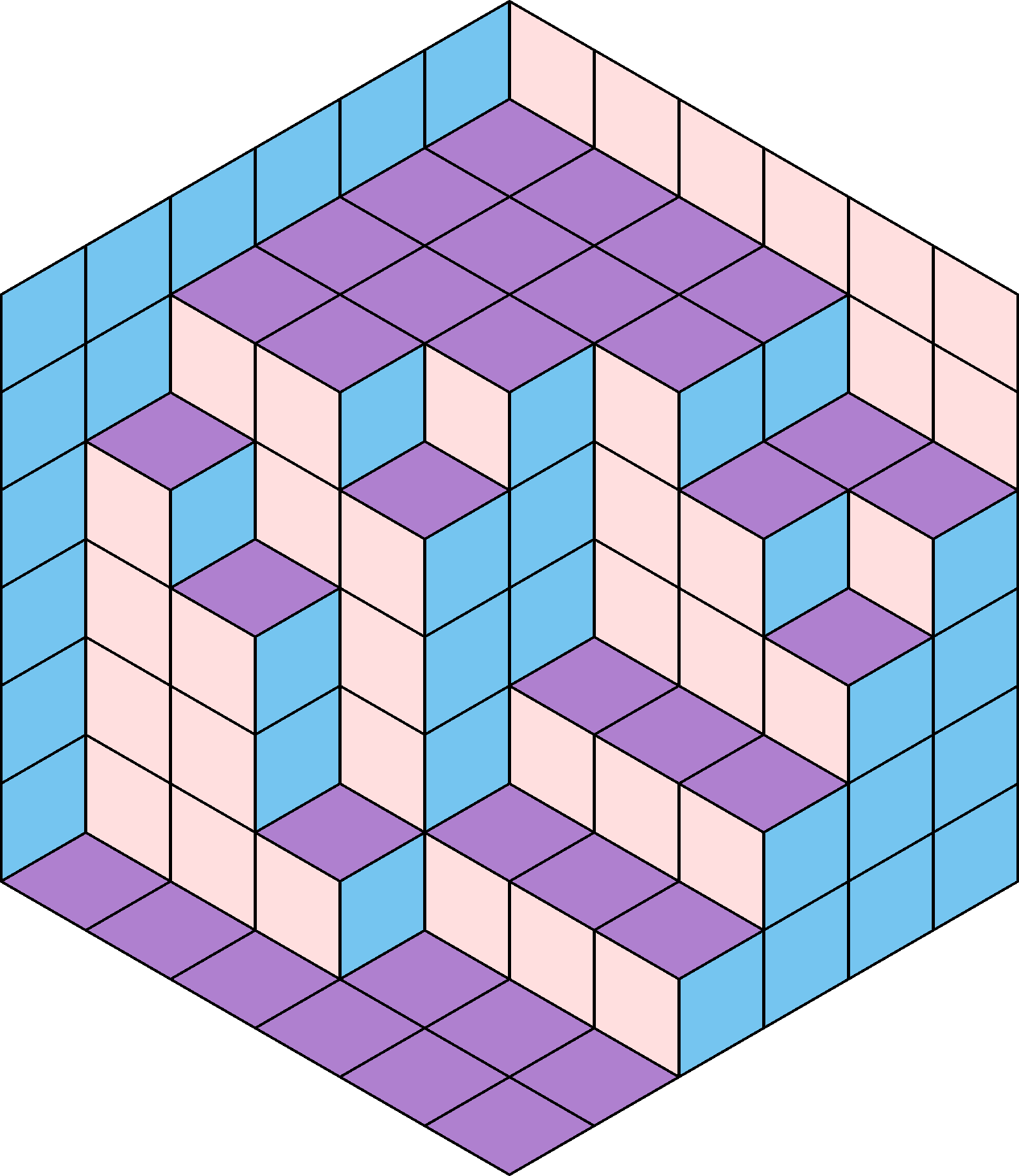Question 54

Challenge question #54 (03/07/2017)

Junior Question

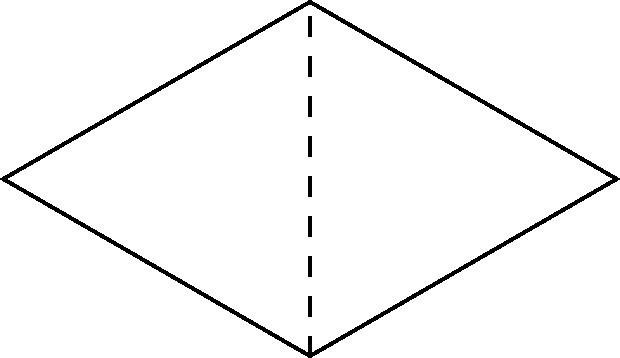A calisson is a French sweet that looks like two equilateral triangles glued together.

Calissons are packed into regular hexagonal boxes, arranged in a way such that there are no gaps between them like in the diagram alongside.

So, there are

3

distinct orientations for the calissons in a box: Maths Image

For any arrangement of the calissons of side length $1$ , find the proportion of each orientation of calisson in a box with side length $6$ .

Answer

Each orientation of calisson takes up $\tfrac{1}{3}$ of the box.

Consider any possible arrangement of the calissons in a box with side length $6$ like the one alongside.

Now suppose we rotate the box $30^{\circ}$ anticlockwise and colour the calissons of the same orientation one colour.

The calissons now appear to form an arrangement of unit cubes within a larger cube of side length $6$ .

If we were to rotate the larger cube such that the pink “walls” are facing up, then the total surface area of the pink “walls” is $6\times 6=36$ .

We can apply a similar argument to the blue “walls” and the purple “floors”.

\therefore\quad

number of pink calissons

=

number of blue calissons

=

number of purple calissons

This argument works for any possible arrangement of calissons.

$\therefore\quad$ each orientation of calisson takes up $\tfrac{1}{3}$ of the box.

Senior Question

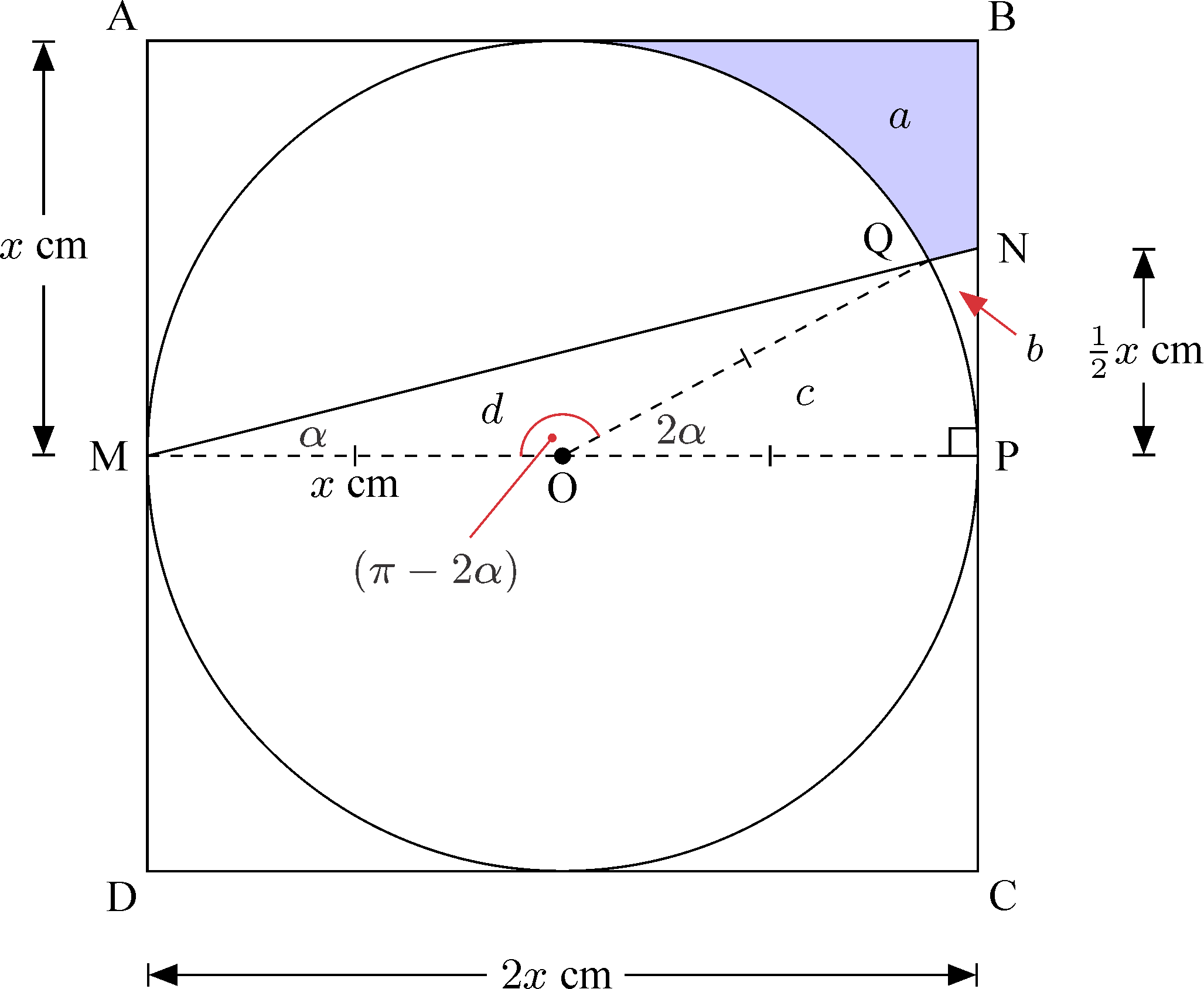
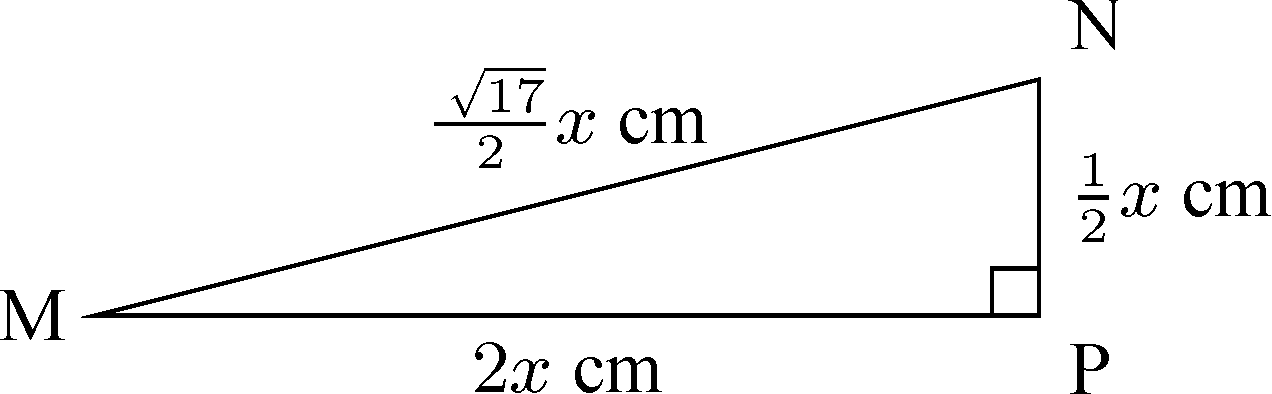
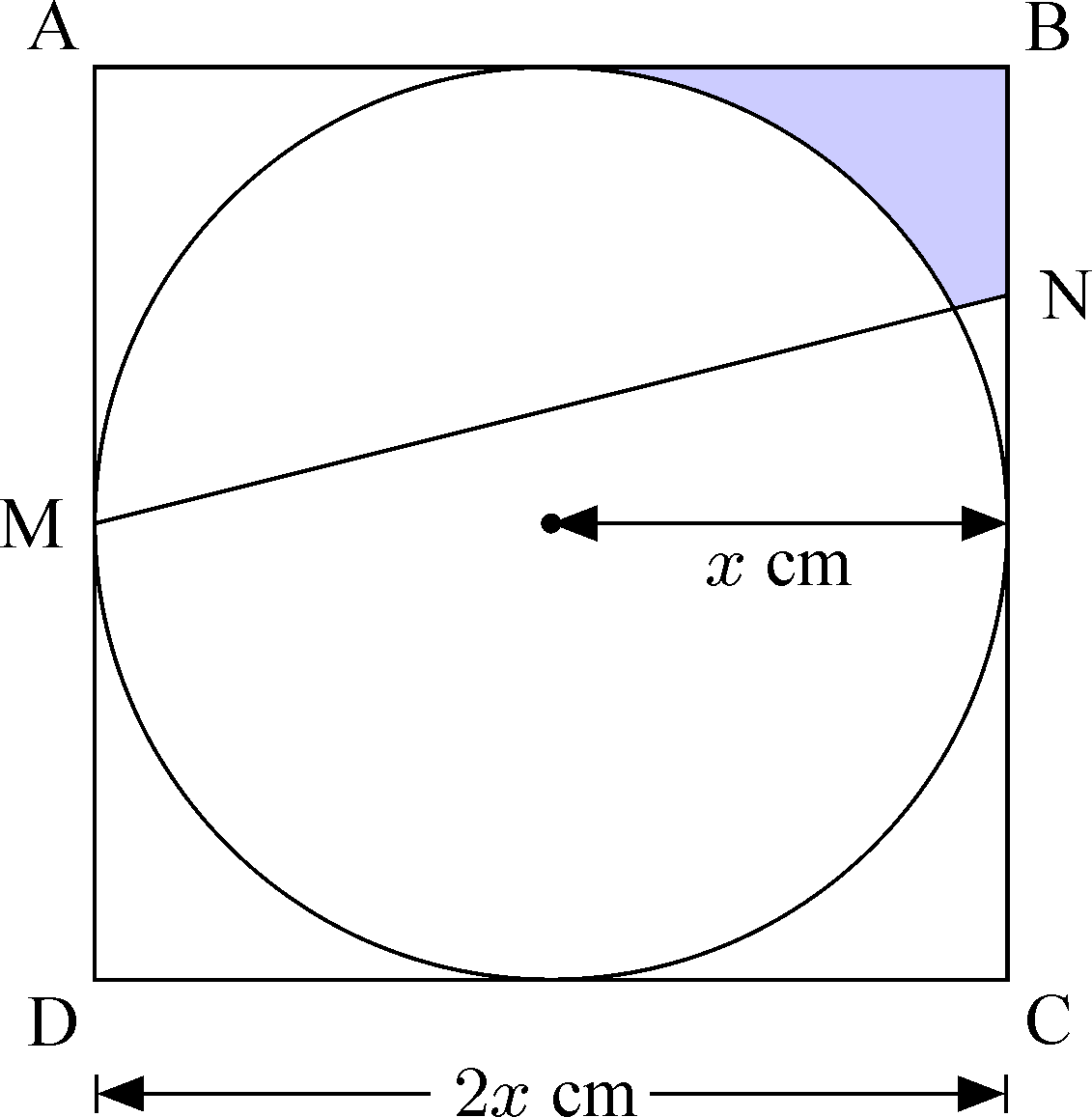A circle with radius

x

cm is inscribed within a square as shown. A line [MN] is drawn where M is the midpoint of [AD] and N is the point on [BC] such that BN

= \tfrac{1}{3}

NC.

Find the shaded area in terms of $x$ .

Answer

shaded area $= x^{2}\left(\tfrac{25}{34} - \tfrac{\pi}{4} + \arctan(\tfrac{1}{4})\right)$ cm $^{2}$

Let O be the centre of the circle and P be a point such that [MP] is the diameter of the circle.

$\therefore\quad$ AM $= x$ cm and NP $=\tfrac{1}{2}x$ cm.

Now

\quad a+b=

area of square

-

area of quarter circle

=

x^{2}-\tfrac{1}{4}\pi x^{2}

=

\left(1-\tfrac{\pi}{4}\right)x^{2}

and

\quad b+c+d=

area of triangle NPM

=

\tfrac{1}{2}\left(2x\right)\left(\tfrac{1}{2}x\right) = \tfrac{1}{2} x^{2}

Let

\quad \text{N}\hat{\text{M}}\text{P} =

\alpha

radians.

\therefore\quad\text{M}\hat{\text{O}}\text{Q} =

\pi - 2\alpha

\{

angles in a triangle

\}

\text{and}\quad \text{Q}\hat{\text{O}}\text{P} =

2\alpha

\{

exterior angle of a triangle

\}

\therefore\quad c=

area of sector OPQ

=\tfrac{1}{2}x^{2}\left(2\alpha\right)

=x^{2}\alpha

and

\quad d =

area of triangle MOQ

=

\tfrac{1}{2}x^{2}\sin\left(\pi - 2\alpha\right)

=

\tfrac{1}{2}x^{2}\sin2\alpha

\therefore\quad b =

\tfrac{1}{2}x^{2}-c-d

=

\tfrac{1}{2}x^{2}-x^{2}\alpha-\tfrac{1}{2}x^{2}\sin2\alpha

=

x^{2}\left(\tfrac{1}{2}-\alpha-\tfrac{1}{2}\sin2\alpha\right)

\therefore\quad a =

\left(1 - \tfrac{\pi}{4}\right)x^{2} - b

=

\left(1 - \tfrac{\pi}{4}\right)x^{2} - x^{2}\left(\tfrac{1}{2}-\alpha-\tfrac{1}{2}\sin2\alpha\right)

=

x^{2}\left(\tfrac{1}{2}-\tfrac{\pi}{4}+\alpha+\tfrac{1}{2}\sin2\alpha\right)

=

x^{2}\left(\tfrac{1}{2}-\tfrac{\pi}{4}+\alpha+\sin\alpha\cos\alpha\right)

Now in triangle MPN,

\tan\alpha =

\dfrac{\tfrac{1}{2}x}{2x} = \tfrac{1}{4}\text{,}\quad\sin\alpha = \tfrac{1}{\sqrt{17}}\text{,}\quad

and

\quad\cos\alpha = \tfrac{4}{\sqrt{17}}

\therefore\quad\alpha=

\arctan\left(\tfrac{1}{4}\right)

\quad a =

x^{2}\left( \tfrac{1}{2} - \tfrac{\pi}{4} + \arctan\left(\tfrac{1}{4}\right) + \left(\tfrac{1}{\sqrt 17}\right)\left(\tfrac{4}{\sqrt 17}\right) \right)

=

x^{2}\left( \tfrac{1}{2} + \tfrac{4}{17} - \tfrac{\pi}{4} + \arctan\left(\tfrac{1}{4} \right)\right)

\therefore\quad

shaded area

=

x^{2}\left(\tfrac{25}{34} - \tfrac{\pi}{4} + \arctan(\tfrac{1}{4})\right)

^{2}